$V$ 君和 $I$ 君在玩一个惊险刺激的游戏。

游戏在一个圆环上进行，圆环上有 $2n$ 个情报站，它们按顺时针依次被标记为 $0,1\dots {2n-1}$，其中编号为奇数的情报站由 $V$ 君控制，其他情报站由 $I$君控制。

这个游戏以情报传递作为背景。$I$ 君已经了解到， $V$ 君在他所控制的情报站之间连接了 $m$ 条通讯线，其中第 $i$ 个通讯线可以看作是连接 $u_i,v_i$ 两点的直线段，它的通讯强度为 $s_i$。$I$ 君希望破坏这些通讯线，为此他可以发射若干束干扰光波。每一束干扰光波需要指定 $I$ 君的两个不同的情报站 $x,y$ 作为发射源和接受源，同时此光波需要指定一个干扰强度 $w$。这样，我们就可以把干扰光波看作一条连接了 $x,y$ 两点、带有权值 $w$ 的直线段。

对于一条通讯强度为 $s$ 的通讯线，设和它相交的干扰光波的集合为 $T$。那么我们认为这个通讯线被破坏，当且仅当 $\sum_{j\in T} w_j\ge s$。

$I$ 君希望破坏 $V$ 君的所有通讯线，然而发射干扰光波是一个很♂累的事情，所以他希望能发射一些合适的干扰光波，使得这些光波的干扰强度之和尽可能小。自然，这个问题将由他的军事参谋——你来负责处理，请你帮 $I$ 君计算出干扰强度之和的最小值，同时给出一种可行的方案。

输入格式

从标准输入读入数据。

第一行两个数 $n,m$，意义如题目描述。

接下来 $m$ 行，第 $i$ 行有三个整数 $u_i,v_i, s_i$，表示第 $i$ 条通讯线连接了 $u_i,v_i$ 两个情报站，通讯强度为 $s_i$，保证 $0\le u_i,v_i < 2n, 1\le s_i\le 10^3$ ，且 $u_i,v_i$ 均为奇数。

输出格式

输出到标准输出。

第一行请输出一个整数 $A$，表示干扰强度之和的最小值。

接下来一行输出一个 $C$，表示你发射的干扰光波个数。

设你的方案中所发射的光波为 $\{(x_i,y_i, w_i)\}$ ，接下来 $C$ 行，每行输出三个空格隔开的整数。其中第 $i$ 行的三个数分别表示 $x_i,y_i,w_i$。

你需要保证以下几点成立，我们才能识别你构造的方案：

• $0\le C\le 10^5$ .

• $\forall 1\le i\le C$ :

  • $0\le x_i, y_i\le 2n, w_i>0$ .
  • $x_i,y_i$ 均为偶数且 $x_i \ne y_i$ .
  • $\sum_{i} w_i \le A$ .

请特别注意：如果你的构造方案不被识别，我们不保证你能获得测试点的部分分。

样例

输入

5 4
1 7 1
9 7 1
3 9 1
5 3 1

输出

2
2
2 8 1
4 6 1

解释

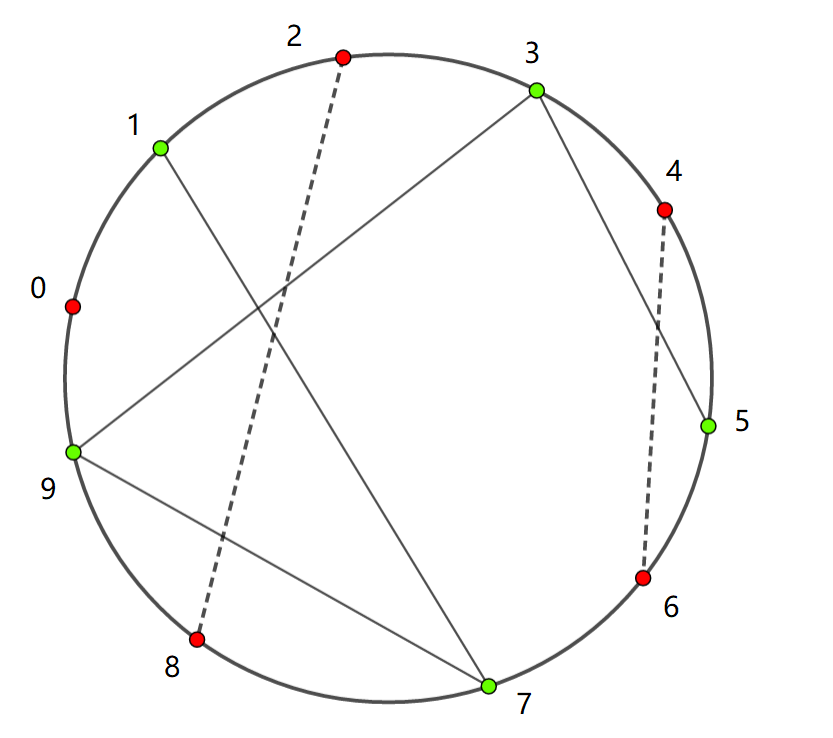
如下图，因为所有通讯强度和干扰强度均为 $1$，故在图中略去。这里绿色点表示$V$君控制的情报站，红色点表示 $I$君控制的情报站，实线表示通讯线，虚线表示干扰光波。注意可行方案不是唯一的。

子任务

• 对于 25% 的数据，满足 $N\le 100, M\le 400$
• 对于另外 25% 的数据，满足 $N\le 500, M\le 10^3$，其中有 5% 的数据还满足 $s_i=1$
• 对于另外 25% 的数据，满足 $N\le 500, M\le 10^4$，其中有 10% 的数据还满足 $s_i=1$
• 对于另外 25% 的数据，满足 $N\le 2000, M\le 4000$, 其中有 10% 的数据还满足 $s_i=1$

在提交代码后将为你评测预测试数据并返回结果。本题的预测试数据包含 $20$ 个测试点，每个测试点和对应的最终评测测试点的 $N,M,s_i$ 的限制相同。

注意：预测试数据的评测结果与最终评测结果没有关系。

评分方式

对每组数据，如果你的程序正确地计算了 $A$ （即干扰强度之和的最小值），得 $3$ 分。若在此基础上给出了一个格式正确、满足要求的构造方案，可以获得 $5$ 分。